Computer programs fundamentally have two interconnected components: Control Flow and Data Transformations. Control flow determines the sequence of operations—essentially deciding which steps happen when, including loops and conditionals. Data transformations handle how information gets processed—converting, combining, or modifying raw data into new forms.

This interdependence becomes critical when things go wrong. Bugs often stem from mismatches between control logic and data handling. Current debugging tools show control flow (which line executes) or data state (variable contents) separately, but struggle with their dynamic relationship. These two aspects interweave constantly in real programs, yet we've lacked a single mathematical framework to capture their interaction.

In the paper "The Compact Double Category Int(Poly*) Models Control Flow and Data Transformations," our researcher Grigory Kondyrev and co-author David Spivak present a wiring diagram syntax that models both aspects in one unified framework. By representing programs as wiring diagrams where control regions contain data paths, we can finally visualize and understand how control structure affects data transformation and vice versa.

Wiring Diagrams: A Visual Language for Computation

The breakthrough comes from a particular kind of wiring diagram—visual representations resembling circuit diagrams that show both the routing of control flow and transformation of data in a single, unified picture.

The example of a wiring diagram looks like this:

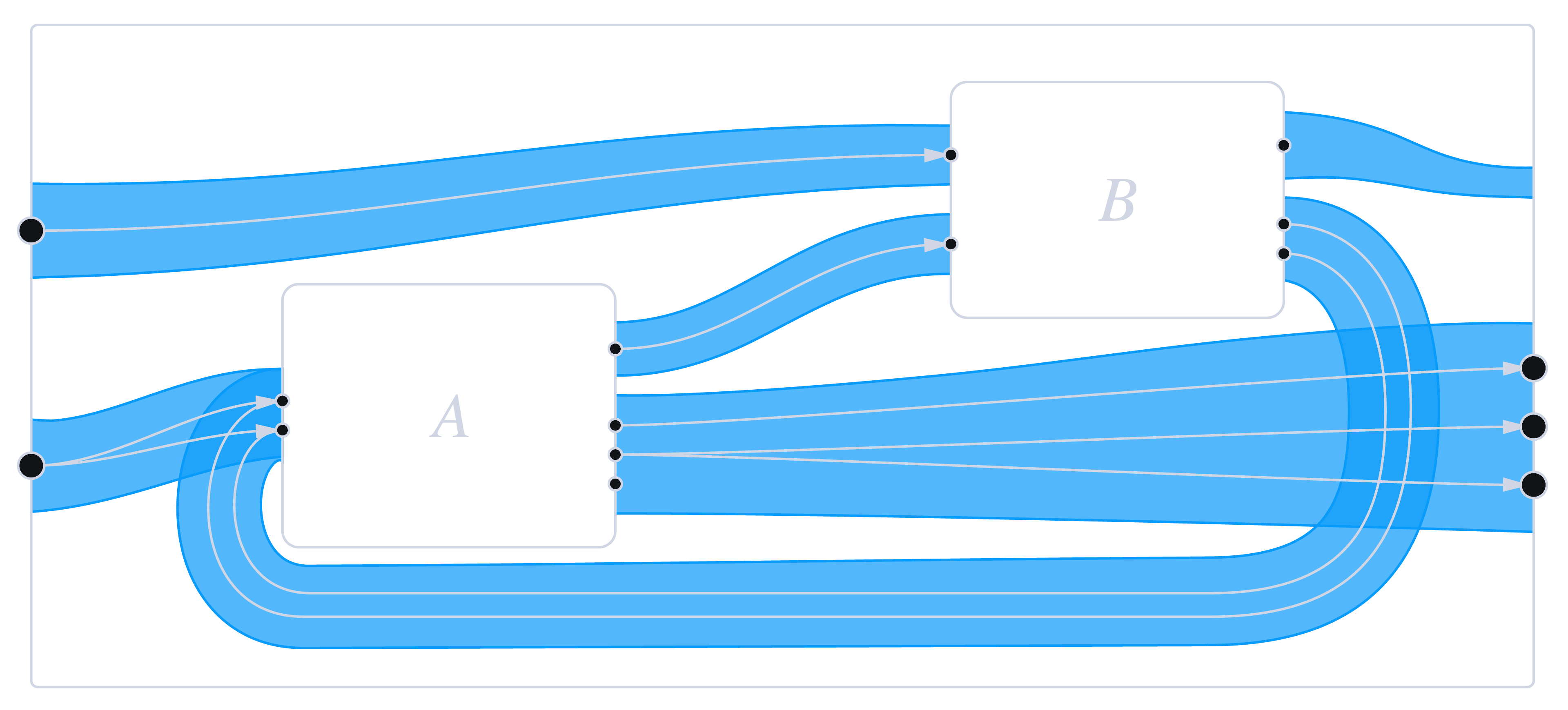
Let's decode what we're seeing: two inner boxes, 𝐴 and 𝐵, within an outer box. Each box represents a computational process with a left side (input) and right side (output). The blue regions represent control flow, showing the possible execution paths after each box completes. The thin white lines are data wires carrying information between processes. Here's how it works: when box A finishes executing, the control flow determines what happens next. If execution flows through the upper blue region, box B becomes active. If it flows through the lower region, data bypasses B and heads directly to the output.

The inputs and outputs of the boxes correspond to so-called polynomial functors, and such visual diagrams correspond to morphisms within the compact double category Int(Poly*). This language captures something previously invisible: how your program's logical structure directly influences what happens to your data, and vice versa.

The Mathematical Foundation

The wiring diagrams unite three separate mathematical research areas into a coherent framework. Masahito Hasegawa's previous work demonstrated that this approach could model programming language control flow [1][2], but only addressed half the story.

Traced Categories for Control Flow: Consider a while loop—the program checks a condition, modifies data, then feeds results back to check again. This "feedback loop" pattern is captured by traced categories, mathematical structures handling situations where outputs loop back as inputs.

Polynomial Functors for both Data and Control Flow: Adding data transformation requires different tools (polynomial functors) that encode how data can be duplicated, deleted, rearranged, and processed. The notation is intuitive: y² represents a signature of a process taking exactly two inputs, while y + y³ represents choosing between one input OR three inputs. This gives precise ways to describe operations like file copying (duplication) or list sorting (rearrangement).

The Int Construction Bridge: The Int construction by Joyal, Street, and Verity [3] provides a way to talk about processes. This technique takes traced categories (modeling control flow) and freely transforms them into compact closed categories with richer compositional properties. These compositional properties allow us to model calling one process within another process.

Applied to polynomial functors, this yields Int(Poly*), simultaneously tracking how control moves through programs and how data transforms at each step. This captures their dynamic interplay that previous approaches missed.

The Main Result: Int(Poly*) as a Universal Framework

This mathematical fusion delivers concrete capabilities that eluded previous approaches. By unifying control flow and data transformation mathematics, Int(Poly*) provides what we believe is the first complete framework for modeling both aspects of computation simultaneously and precisely.

1. Referential Transparency with Imperative Power: The framework achieves referential transparency (same input always produces same output with no hidden side effects) combined with imperative power (ability to directly command and modify program execution). You get both the clean mathematical reasoning of functional programming and the direct control of imperative programming. 2. Visual Syntax: Complex processes become intuitive wiring diagrams that nest compositionally—smaller diagrams embed within larger ones. 3. Universal Properties: The framework satisfies universal properties from category theory, meaning it's not just one possible approach but the "canonical" way to model these interactions.

Beyond basic capabilities, Int(Poly*) extends to a double category tracking both static wiring patterns and dynamic control trajectories. This enables "segmentation", which factors complex control flow into simpler components for precise trajectory tracking through wiring diagrams.

Practical Impact and Future Directions

Immediate Applications: Visual debugging tools showing data flow and control movement simultaneously; new programming language designs naturally expressing control-data interplay; formal verification and optimization tools; intuitive educational approaches making programming concepts concrete.

Future Extensions: The mathematical machinery is flexible enough to extend to concurrent and distributed systems, quantum computing, and machine learning architectures. It can adapt to any computational paradigms that emerge.

The Bigger Picture

Looking ahead, as we develop increasingly complex autonomous systems and algorithmic agents, we'll need mathematical tools that can provide provable guarantees about behavior. A mathematical framework like Int(Poly★) offers a path forward, allowing us to reason rigorously about systems whose complexity would otherwise overwhelm conventional analysis.

The wiring diagrams may seem simple, but they encode profound truths about computation's nature. By making these truths visible and mathematically precise, this work provides new ways to think about, design, and understand the programs shaping our world.

Check out the full paper on arXiv here: https://arxiv.org/abs/2509.05462